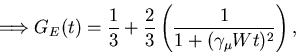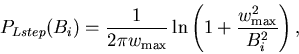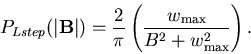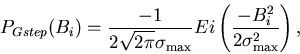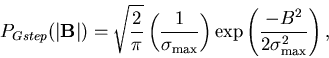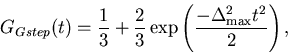

Next: Incommensurate Magnetic Ordering
Up: An Ornamental Garden of Field Distributions and Static
Previous: Lorentzian distribution of Lorentzians
Monotonic decreasing distributions of magnitude of field are easy to write
down (they may be hard to justify in a physical model of a material, and the
corresponding component distributions are sometimes not easy to identify).
For the exponential
by direct integration
a monotonic Lorentzian relaxation shape.
If the standard Lorentzian field distribution, with width parameter w, is
convoluted with a step function:
then
This process creates a simple Lorentzian distribution for the magnitude of
field, and reveals the corresponding component distribution. The Fourier
transform of a simple Lorentzian is well known to be an exponential, so by
direct integration:
The convolution has preserved the Lorentzian pathology, the second moments
diverge, and the initial slope of the relaxation is nonzero.
Similarly, convoluting
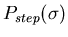 with the standard Gaussian field
distribution results in:
with the standard Gaussian field
distribution results in:
where Ei(x) is the exponential-integral function as defined by Gradshteyn
and Ryzhik,[4]
where
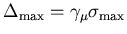 .
Again the convolution
with the step function has turned the magnitude distribution into the
functional form normally associated with the component distribution, and
also generated its component distribution. In both cases, the component
distribution diverges logarithmically as
.
Again the convolution
with the step function has turned the magnitude distribution into the
functional form normally associated with the component distribution, and
also generated its component distribution. In both cases, the component
distribution diverges logarithmically as
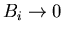 .
.


Next: Incommensurate Magnetic Ordering
Up: An Ornamental Garden of Field Distributions and Static
Previous: Lorentzian distribution of Lorentzians
Jess H. Brewer
2002-09-24