BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: Fudging The Bohr Atom
Up: Particle in a Box
Previous: Particle in a Box
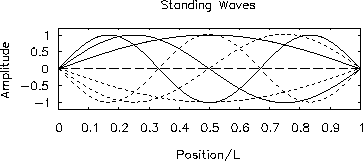
Figure:
-
First three allowed modes of a standing wave
confined to a 1-dimensional box.
 |
Suppose an electron is confined somehow to a ``1-dimensional box''
(like a bead on a wire). Actually there are many examples of
such systems; a DNA molecule is an interesting example.
The ``box'' (or string, or however you want to think of it)
has a length  .
If the electron is truly
confined to the box, then its ``wave'' must have
nodes (zeroes) at the ends of the box
-- and be zero everywhere outside the box.
This is the familiar condition defining the allowed ``modes''
of vibrations in a string or in a closed organ pipe:
.
If the electron is truly
confined to the box, then its ``wave'' must have
nodes (zeroes) at the ends of the box
-- and be zero everywhere outside the box.
This is the familiar condition defining the allowed ``modes''
of vibrations in a string or in a closed organ pipe:
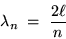 |
(24.2) |
where n is any nonzero integer.
If we put this together with de Broglie's formula (1),
we get an equation for the momentum of the electron
in it's
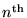 mode:
mode:
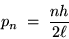 |
(24.3) |
and if we recall that the kinetic energy associated with
a particle of mass m having momentum p is given by
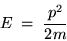 |
(24.4) |
then we have the energy of the electron in its
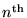 mode:
mode:
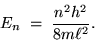 |
(24.5) |
The electron not only has discrete ``energy levels''
but it has an irreducible minimum energy for the
lowest possible state (the `` GROUND STATE''):
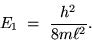 |
(24.6) |
The smaller the box, the bigger the ground state energy.
Particles don't ``like'' to be confined!
This has a number of profound consequences which we will revisit shortly.
But first let's do a little trick and turn our string into a
circle . . . .


Next: Fudging The Bohr Atom
Up: Particle in a Box
Previous: Particle in a Box
Jess H. Brewer
2000-01-17
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE ![]() mode:
mode: