 is defined by its properties:
is defined by its properties:
The so-called Dirac delta function  is defined by its properties:
is defined by its properties:
 .
.
 .
(This makes mathematicians very uncomfotable; they prefer to call
.
(This makes mathematicians very uncomfotable; they prefer to call
 a ``distribution'' rather than a ``function.'')
a ``distribution'' rather than a ``function.'')
 .
.
It has a number of handy representations:
 .
.
 .
.
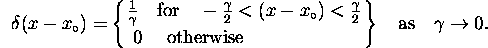
 .
.