
(Turn in Mon 21 Sep)
Write a sentence describing what is hardest about the 2nd half of the chapter.
Obviously there is no "correct answer" for this sentence.
| 32: Two waves on a string travel in opposite directions at 100 m/s. The figure shows a snapshot graph of the string at t = 0, when the two pulses overlap, and another snapshop graph of the left-going pulse at t = 0.050 s. Draw a snapshot graph of the right-going pulse at t = 0.050 s. |

|
We naturally assume that both ends of the string are fixed,
so that the ends are nodes (zero amplitude & zero phase at x = 0).
The amplitude is 1/2 its maximum value when sin(k x) = 0.5,
i.e. when k x = 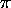 /6 = 30o
or
/6 = 30o
or 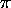 /6 + any integer multiple of
/6 + any integer multiple of
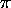 . Thus for x = 0.3 m,
we have the desired condition for
(0.3 m) k = (n + 1/6)
. Thus for x = 0.3 m,
we have the desired condition for
(0.3 m) k = (n + 1/6) 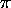 .
Since k = 2
.
Since k = 2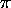 /
/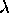 ,
this implies
,
this implies 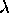 = (0.6 m)/(n + 1/6).
The string is vibrating at its third-harmonic frequency, meaning
that there are two nodes and three half-wavelengths between the ends,
or that the length of the string is
L = 3
= (0.6 m)/(n + 1/6).
The string is vibrating at its third-harmonic frequency, meaning
that there are two nodes and three half-wavelengths between the ends,
or that the length of the string is
L = 3 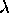 /2, or
/2, or
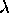 = 2L/3 = (0.6 m)/(n + 1/6).
Simplifying, we have L = (0.9 m)/(n + 1/6).
The simplest case is of course for n = 0, giving
L0 = 5.4 m; the next possibility (for n = 1)
is L1 = 0.77142857 m; for n = 2 we get
is L2 = 0.41538462 m; and so on.
= 2L/3 = (0.6 m)/(n + 1/6).
Simplifying, we have L = (0.9 m)/(n + 1/6).
The simplest case is of course for n = 0, giving
L0 = 5.4 m; the next possibility (for n = 1)
is L1 = 0.77142857 m; for n = 2 we get
is L2 = 0.41538462 m; and so on.
| 46: The two strings are of equal length and are being driven at equal frequencies. The linear density of the left string is 2.0 g/m. What is the linear density of the right string? |

|
| 50: The tube is filled with pure oxygen and the piston is driven at 400 Hz. What is the speed of sound in oxygen? |

|