- . . . FORCE,17.1
- The
COULOMB FORCE law, like the ``coulomb'' unit for electric charge
(to be discussed later), is named after a guy called Coulomb;
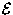 &
&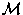 units are littered with the names of the people who invented
them or discovered related phenomena. Generally I find this
sort of un-mnemonic naming scheme counterdidactic, but since we
have no experiential referents in
units are littered with the names of the people who invented
them or discovered related phenomena. Generally I find this
sort of un-mnemonic naming scheme counterdidactic, but since we
have no experiential referents in 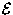 &
&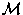 it's as good a scheme as any.
it's as good a scheme as any.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . other.17.2
- On a
microscopic scale there are serious problems
with this picture. As the two charges get closer together,
the force grows bigger and bigger and the work
required to pull them apart grows without limit;
in principle, according to Classical Electrodynamics,
an infinite amount of work can be performed by two
opposite charges that are allowed to ``fall into''
each other, providing we can set up a tiny system
of levers and pulleys. Worse yet, the ``self energy''
of a single charge of vanishingly small size
becomes infinite in the classical limit. But I am
getting ahead of myself again . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . atom.17.3
- Now I am 'way ahead
of myself; but we do need something for an example here!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . there!]17.4
- We
often try to represent this graphically by drawing
``lines of force'' that show which way
 points
at various positions; unfortunately it is difficult
to draw in
points
at various positions; unfortunately it is difficult
to draw in  at all points in space.
I will discuss this some more in a later Section.
at all points in space.
I will discuss this some more in a later Section.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . decide.17.5
- Define ``real.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . magnitude.17.6
- A
force perpendicular to the motion does no work on the
particle and so does not change its kinetic energy or speed
- recall the general qualitative features of CIRCULAR MOTION
under the influence of a CENTRAL FORCE.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
reads17.7
- In ``practical'' units the formula reads
where cm are (as usual) centimeters, MeV/c are millions of
``electron volts'' divided by the speed of light (believe it or not,
a unit of momentum!) and kG (``kilogauss'') are thousands of Gauss.
I only mention this now because I will use it later on and because
it illustrates the madness of electromagnetic units - see next Section!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . flow17.8
- For instance, the flux of a
river past a fixed point might be measured in gallons per minute
per square meter of area perpendicular to the flow. A hydroelectric
generator will intercept twice as many gallons per minute if it
presents twice as large an area to the flow. And so on.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . fields,17.9
- Note that, just as in the case of the
mechanical potential energy V, the zero of
 is chosen arbitrarily at some point in space; we are really
only sensitive to differences in potential. However,
for a point charge it is conventional to choose an infinitely
distant position as the zero of the electrostatic potential,
so that
is chosen arbitrarily at some point in space; we are really
only sensitive to differences in potential. However,
for a point charge it is conventional to choose an infinitely
distant position as the zero of the electrostatic potential,
so that  for a point charge Q is the work required
to bring a unit test charge up to a distance r away from Q,
starting at infinite distance.
for a point charge Q is the work required
to bring a unit test charge up to a distance r away from Q,
starting at infinite distance.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . before,17.10
- Remember the metaphor of
 as the ``slope'' of a ``hill'' whose height is given by
as the ``slope'' of a ``hill'' whose height is given by
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . charge17.11
- This is what we mean when we say
that charge is quantized.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . weird.17.12
- And also, I suspect, because people
were looking for a good way to honour the great Physicist
Ampère and all the best units were already taken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE