- ... Arithmetic.4.1
- No doubt
the useful lifetime of this example is only a few more years,
since many students now learn to divide by punching the right
buttons on a hand calculator, much to the dismay of their
aged instructors. I am not so upset by this - one arithmetic
manipulation technology is merely supplanting another -
except that ``long division'' is in principle completely
understood by its user, whereas few people have any idea what
actually goes on inside an electronic calculator.
This dependence on mysterious and unfamiliar technology may have
unpleasant long-term psychological impact, perhaps making us
all more willing to accept the judgements of authority figures
without question.... But in Mathematics, as long as you have
once satisfied yourself completely that some technology
is indeed trustworthy and reliable, of course you should make
use of it! (Do you know that your calculator always
gives the right answers...?)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... teachers!4.2
- It
occurs to me that Grammar school is called Grammar school
because it is where we learn grammar - i.e. the
conventional representations for things, ideas and
the relationships between them, whether in verbal language,
written language, mathematics, politics, science or social
behaviour. These are usually called ``rules'' or even (when
a particularly heavy-handed emphasis is desired) ``laws''
of notation or manipulation or behaviour. We also pick up
a little technology, which in this context begins to
look pretty innocuous!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... number4.3
- I
do not know the proof that
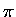 is an irrational number,
but I have been told by Mathematicians that it is,
and I have never had any cause to question them.
In principle, this is reprehensible (shame on me!)
but I am not aware of any practical consequences
one way or the other; if anyone knows one, please set me straight!
is an irrational number,
but I have been told by Mathematicians that it is,
and I have never had any cause to question them.
In principle, this is reprehensible (shame on me!)
but I am not aware of any practical consequences
one way or the other; if anyone knows one, please set me straight!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scale.4.4
- For
instance, it explains easily why the largest animals on Earth
have to live in the sea, why insects can lift so many times their
own weight, why birds have an easier time flying than airliners,
why bubbles form in beer and how the American nuclear power
industry got off to a bad start. All in due time....
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Laws:4.5
- Note
that division is not commutative:
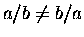 ! Neither is subtraction,
for that matter:
! Neither is subtraction,
for that matter:
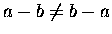 .
The Commutative Law for multiplication, ab=ba, holds for ordinary
numbers (real and imaginary) but it does not necessarily
hold for all the mathematical ``things'' for which some form of
``multiplication'' is defined! For instance, the group
of rotation operators in 3-dimensional space is not
commutative - think about making two successive rotations of a
rigid object about perpendicular axes in different order and
you will see that the final result is different! This seemingly
obscure property turns out to have fundamental significance.
We'll talk about such things later.
.
The Commutative Law for multiplication, ab=ba, holds for ordinary
numbers (real and imaginary) but it does not necessarily
hold for all the mathematical ``things'' for which some form of
``multiplication'' is defined! For instance, the group
of rotation operators in 3-dimensional space is not
commutative - think about making two successive rotations of a
rigid object about perpendicular axes in different order and
you will see that the final result is different! This seemingly
obscure property turns out to have fundamental significance.
We'll talk about such things later.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Theorem:4.6
- Surely you aren't going
to take my word for this! Convince yourself
that this formula is really true!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... consistent4.7
- In
Mathematics we never worry about such things;
all our symbols represent pure numbers;
but in Physics we usually have to express
the value of some physical quantity in units which
make sense and are consistent with the units of other
physical quantities symbolized in the same equation!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... generally4.8
- The
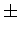 symbol means that both signs (+ and -)
should represent legitimate answers.
symbol means that both signs (+ and -)
should represent legitimate answers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE