Introduction

Whenever someone measures a physical quantity--for example, a length measured by putting a ruler beside it or a mass measured by comparing it with known masses on a balance­­there is some range of uncertainty in the result. No quantity is ever measured with complete precision. In the examples cited, one can imagine some reasons for the uncertainty. Limitations of eyesight make it impossible to tell precisely where the end of the object falls on the ruler. If the length is read to be 10.25 cm, it could actually be l0.255 cm or 10.245 cm and look exactly the same to the eye. Similarly, there will be a range within which mass may be added or subtracted from the balance pan without upsetting the appearance of balance. Such effects will lead with equal probability to measurements that are too high or too low, and a single observer will probably get different values within the range of uncertainty for successive measurements. Errors of this sort are referred to as random. There may also be sources of systematic error which lead consistently to a number which is too large or too small. This could happen, for instance, with a wooden ruler which had absorbed water on a humid day and increased its length or with a balance which had not been properly balanced when both pans were empty. Systematic errors are more difficult to detect than random errors because they do not produce different values for successive measurements. Nevertheless, the validity and usefulness of an experiment depends critically on the proper assessment of systematic errors.

Probability Distribution

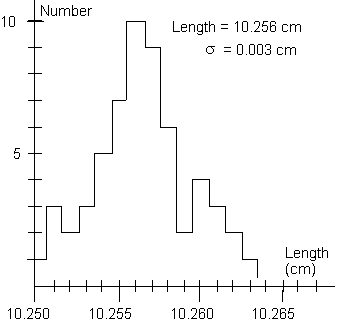
The uncertainty associated with random error may be estimated by making a measurement several times and considering the distribution of results. It is often convenient to display the distribution graphically as in Figure 1, where we have plotted on the horizontal axis the measured value of a length and on the vertical axis the number of times a particular value, or range of values within a given bin, was measured. This type of graph is called a histogram.

Length (cm)	Number of Times Measured
10.250	1
10.251	3
10.252	2
10.253	3
10.254	5
10.255	7
10.256	10
10.257	9
10.258	6
10.259	2
10.260	4
10.261	3
10.262	2
10.263	1

Figure 1

Figure 1 illustrates a common property of such a series of measurements. The values usually tend to cluster around a central value, in this case around 10.256 cm, showing a "peak" of high probability for measuring values close to the center and showing fairly symmetrical "tails" of low probability for values far from the center.

Given the data shown in Figure l, what can we conclude about the true value of the length being measured? Can we say only that the length is somewhere between 10.250 cm and 10.263 cm? While it is probable that the true value lies somewhere within this range, it is most likely that it is somewhere near the center of the distribution. Our best guess for the true value will be the average (or mean) of the distribution, which is defined as

,

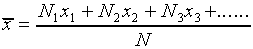where 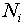is the number of times the value 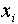occurs and where N is the total number of measurements,

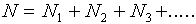
The most common way of assigning a size to the uncertainty associated with random error in a single measurement is to calculate the standard deviation 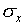of the distribution from the formula

,

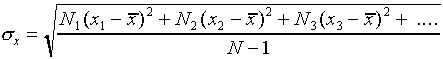or equivalently

.

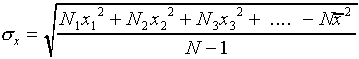The standard deviation is a measure of the uncertainty associated with a single measurement. A typical measurement can be expected to be about a standard deviation away from the mean value. Of course, some measurements have a smaller difference from the mean than 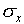and some have a larger difference. Sometimes one uses the relative error (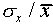, written as a percentage) to express the uncertainty in a single measurement. For the data of Figure 1, 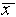= l0.256 cm, 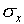= 0.003 cm, and / 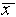= 0.0003 = .03%. Having guessed that, of all the estimates discussed, the mean value of the distribution of measurements is closest to the true value of the quantity, we can ask "How much confidence should we have in this guess?" The answer is given by statistical theory: the average difference of the mean from the true value is of a size 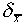given by

.

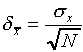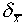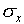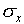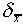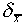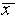This number is often called the standard deviation of the mean, but it is important to distinguish it from the standard deviation of a single measurement. If we were to take more measurements (i.e., increase N), should not change much, but would become smaller. We often use this quantity as an error figure to accompany a measured number, so that x = 5.7 ± 0.2 cm means that the best estimate is = 5.7 cm and the uncertainty associated with this estimate is 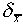= 0.2 cm.

Normal Distribution

According to statistical theory, a measured probability distribution such as Figure 1 can be approximated by a "normal distribution function"

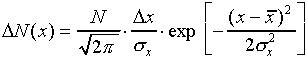
where is the number of measurements between x and x + x and where N is the total number of measurements. and 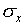are the mean and the standard deviation. The notation "exp[...]" means raise the quantity 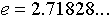to the power given in the square brackets. The normal distribution function is plotted in Figure 2.

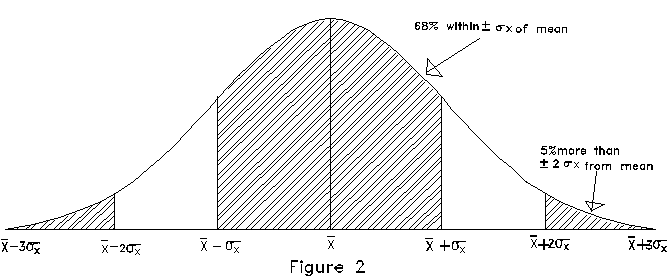
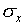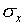Note again that there are long tails, indicating that a small fraction of the measurements will be much more than away from the mean value. For the normal distribution, 5% of the measurements will be more than ±2 away from 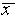while 68% are within of 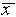. This well-known distribution is also sometimes called the "Gaussian" distribution or the "Bell-curve."

Subjectively Estimated Errors

Sometimes it is not practical to make the large number of measurements needed to calculate accurate estimates of the mean and standard deviation; instead, just one measurement is available to use as the estimate of the true value. In this case you must use your judgment to estimate the uncertainty in this measurement. Several factors may enter into this, some of which could be the following:

1) The uncertainty may come from how accurately you feel you can read a measuring device. For example, the accuracy with which you could read a ruler would depend on how closely spaced its tick marks are, and on how steadily it could be held while the measurement was being made.

2) There may be fluctuations in the conditions under which an experiment was done which could affect the outcome of the experiment but which were beyond the control of the observer. These might include variations in temperature or line voltage.

3) Your model of the physical situation may be somewhat unrealistic, so that no matter how precisely measurements are made, calculations using these measurements will not give an accurate result because the formulas aren't a totally accurate model of reality. An example of this would be a calculation of the range of a projectile using a formula that neglects air resistance: the result might be fairly accurate for a bullet but not for a wad of paper, no matter how precisely you measure its initial velocity.

You must take the various factors into consideration and then exercise your best judgment in estimating the range within which you are confident that the measurement lies. The hope is that for random errors the estimate of the uncertainty that you make this way would be comparable to the value of 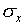you would obtain if you made the measurement several times.

Propagation of Errors

Once the uncertainty in a measured quantity x has been found, it is often necessary to calculate the consequential uncertainty in some other quantity which depends on x. Consider a function f which depends on x and/or y: .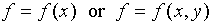

A series of measurements of x and/or y will yield 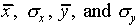. We will assume that the best estimate of f is 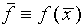or . (But note that 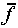defined this way is not always the same as the mean of f obtained from the individual value .)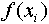

Examples of the way to find 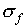, the standard deviation of f, are given below:

(a)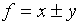

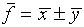
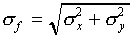
(The standard deviation for f is obtained by adding the standard deviations for x and y "in quadrature.")

(b)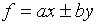

(c)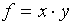

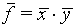
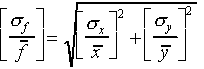
(The relative error for f is obtained by adding the relative errors for x and y "in quadrature")

(d)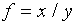

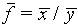
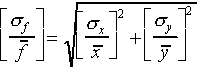
(e)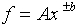

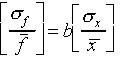
where A and b are precisely­known constants and b is positive.

(The relative error for f is b times the relative error for x.)

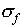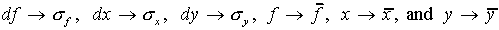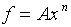The rules for calculating need some explanation. Let df be the small change in f which results from small changes dx, dy in the quantities x, y. One can then make the identifications: . For example, let . Then,

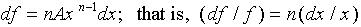
With the above identifications, we obtai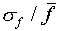n () = n(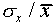). As another example, let 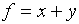. Then 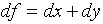. We might conclude that . However, during half of the time, the deviations in x and y will be in opposite directions (as long as x and y are measured independently) so that one expects 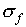to be less than 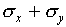. A careful statistical analysis shows that 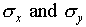should be added "in quadrature." All the rules (a) through (e) can easily be obtained by identifying differentials with standard deviations and by replacing addition or subtraction by addition "in quadrature."

PART I SHOULD BE COMPLETED BEFORE COMING TO THE LAB.

A. Consider a solid metal ball of mass M and diameter D. You are given the problem of determining the density of the metal by measuring M and D.

density =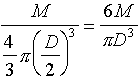

The ball's mass is measured with a simple laboratory balance, and the following results are obtained for M:

927 gm 929 gm 925 gm 927 gm 928 gm

929 gm 930 gm 928 gm 929 gm 927 gm

The ball's diameter is measured with a vernier caliper, and the following results are obtained for D:

5.88 cm 5.83 cm 5.83 cm 5.85 cm 5.83 cm

5.81 cm 5.82 cm 5.84 cm 5.83 cm 5.82 cm

(a) Plot a histogram of the distribution of the ten values for M, and find the mean value and the standard deviation of the distribution.

(b) Do the same for the distribution of D values.

(c) Determine the density of the metal, and indicate the uncertainty in your value.

B. Estimate the density of your own body. Do this by first estimating the volume of your body, thinking of it as an assemblage of cylinders, spheres, truncated cones, etc., and make the measurements necessary to estimate the volume of each part. Note that the volume of a truncated cone,

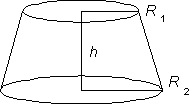
is .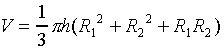

Your estimate of the uncertainty of the volume will not be determined by calculating a standard deviation, since you need to make each measurement only once, but rather by estimating the accuracy of each measurement and of the model. Divide your total volume into your mass (an object that weighs 2.2 lbs. on earth has a mass of 1 kg.) to obtain an estimate of your density. Compare this with the density of water. Do you float or sink in fresh water?

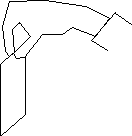
A. Measure your reaction time by trying the following: smooth out a dollar bill and have a friend hold it vertically as shown. Put your thumb and index finger on either side of the bill without touching it, about halfway down for the first trial. When your friend releases the bill try to catch it. (Do you see the makings of a good bet here?) On subsequent trials, find out how far down the bill you have to place your fingers in order to catch it, and estimate the uncertainty in this. Use 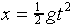to calculate an estimate of your reaction time, and calculate the uncertainty in this estimate.

B. Now measure your reaction time by using a digital electronic timer in "sensed start/stop" mode. In this mode, the timer starts when one light beam is interrupted and stops when the other light beam is interrupted. See how soon after someone starts the timer that you can stop it. Repeat the measurement a few times. Is the result of these measurements consistent with the estimate of your reaction time and its uncertainty made using the dollar bill?

As a way of generating data with a spread about a central value, throw darts at the target (aiming for the central square) and record the number of hits within each square. Throw at least 100 darts, more if you have the patience. (The target is on the last page of this experiment.)

Add up the total number of hits on each row of the target. Find the mean vertical position 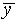and the standard deviation 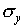. Make a histogram of the y distribution and include on the graph a normal distribution curve which has the same values of 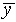and 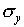. How well does this curve match your experimental distribution? Is your value of 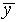at the center, within the expected uncertainty? (If it is not, does this mean that you are not aiming right?)

Now add up the total number of hits on each column of the target, and repeat the previous exercise for the x distribution.

You now have your accuracy in the vertical and horizontal directions (by the numbers 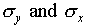). Why should you expect these two numbers to be, or not to be, the same?

Geiger counters are provided to detect particles emitted from radioactively decaying nuclei. A given nucleus decays at a random time which cannot be predicted in advance. Thus, the distribution of decays from a radioactive source will show statistical fluctuations in time.

Measure the number of decays D registered by the Geiger counter in a 15­second time interval. Make this measurement a total of twenty times. Calculate 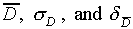from your twenty values for D.

Statistical theory predicts that 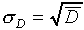for this sort of random event (characterized here by the fact that the probability that any one nucleus decays in a given time interval is very small ­ this sort of probability distribution is called a Poisson distribution). Do your results approximately agree with this?