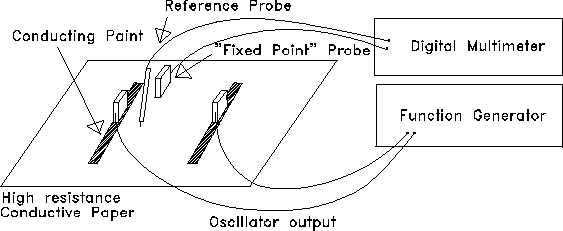
Figure 5.1: Apparatus for measuring electric potential in two dimensions.
There is no simple and sufficiently sensitive device which permits the measurement of the electric field intensity at a point in the free space surrounding a system of electrically charged conductors. Instead, we will study fields in two dimensions, on a sheet of high resistance slightly-conducting paper. The experimental setup is shown in the figure below. The source of the charges is a 60 Hz oscillator (function generator). Wires from the oscillator are attached to electrodes having protruding pins, which are then connected directly into the paper or into large conductors which have been painted on the paper. Minute electric currents are established in the paper along the electric field lines between the point charges or painted conductors. The field can then be studied using two probes connected to a digital voltmeter (DVM). To do this, the probes are placed at two points on the paper, with the voltmeter then indicating the potential difference between the two points. When the voltmeter reads 0 Volts, there is no potential difference between the probes and therefore the probes lie at two points on the same equipotential "surface" (in two dimensions, an equipotential curve). Since the electric field is everywhere orthogonal to the equipotential curves, the field lines can be mapped once several equipotential curves have been delineated.

Figure 5.1: Apparatus for measuring electric potential in two dimensions.
To plot each equipotential curve, a ``fixed point'' probe is inserted at some point, while a reference probe is moved to locate the points at which a null potential difference is obtained. The locus of these equipotential points should be marked on the conducting paper. To plot a new equipotential curve, the fixed point probe is moved to another point and the process is repeated.
The experimental arrangement imposes a distortion in plotting the field distribution. Since currents are confined to the paper itself, the current (and therefore the field) at the edge of the paper is always parallel to the edge. Hence distortion of the field near the edge of the paper must be expected. Whatever the directions of the equipotential surfaces might be in an unlimited medium, they will always be found perpendicular to the edge of the paper and therefore distorted into this direction over a considerable distance away from the edge.
The various shaped conductors are painted onto the coated paper using highly conductive paint. Note that to be effective this paint must be applied in a uniform layer and allowed to dry for at least ten minutes.
You will study the field of two point charges of equal magnitude-both in the case that the point charges are of opposite sign and in the case that they are of the same sign-and you will study the field between two parallel conducting plates. You will also verify the following theorem:
If a hollow conductor of arbitrary shape is placed in an electric field
and if there are no charges in the cavity of the conductor, then the field
in the cavity is zero. It follows that the interior of the cavity is an e
quipotential region, i.e., all points in the cavity are at the same
potential as the conductor itself.
Finally, you will make quantitative measurements of the field's dependence on distance in the region between two parallel conducting plates.