It is plausible that the notion of Cooper pairing and BCS theory may still be applicable to the high-temperature superconductors, yet the nature of the pairing mechanism may be something other than the phonon-induced electron-electron interaction. The formation of a bound state can be achieved by any attractive interaction capable of overcoming the natural Coulomb repulsion between two electrons. Several alternative sources for this attractive force which are compatable with conventional BCS theory have been proposed. One such mechanism, which has received much attention in recent years, is an electron-electron interaction mediated by magnetic spin fluctuations [51,52,53]. The concept is not entirely new. A similar process is believed to help facilitate p-wave spin-triplet pairing (L=1, S=1) in superfluid 3He, and to lead to other pairing states in certain organic superconductors and heavy fermion systems such as UPt3 [49,53].
The antiferromagnetic state
of the parent materials such as
![]() and the anomalous
normal-state properties of the high-Tc superconductors provide
the inspiration for attempts at describing the superconducting properties
in terms of a spin-fluctuation exchange
mechanism [52,53,82]. A logical starting point
for such a theory
is to suggest that the physical origin of those normal-state features
which differ from normal metals may somehow be responsible for
superconductivity in the cuprates. It has been suggested that the
measured anomalous normal-state properties of
and the anomalous
normal-state properties of the high-Tc superconductors provide
the inspiration for attempts at describing the superconducting properties
in terms of a spin-fluctuation exchange
mechanism [52,53,82]. A logical starting point
for such a theory
is to suggest that the physical origin of those normal-state features
which differ from normal metals may somehow be responsible for
superconductivity in the cuprates. It has been suggested that the
measured anomalous normal-state properties of
![]() stem from strong antiferromagnetic correlations of spins, and these
same antiferromagnetic spin fluctuations are also responsible for
superconductivity in the cuprates [1]. NMR measurements
of the normal state have been successfully modelled with a
nearly antiferromagnetic Fermi liquid [55,56,57].
stem from strong antiferromagnetic correlations of spins, and these
same antiferromagnetic spin fluctuations are also responsible for
superconductivity in the cuprates [1]. NMR measurements
of the normal state have been successfully modelled with a
nearly antiferromagnetic Fermi liquid [55,56,57].
Some insight into the origin of possible antiferromagnetic spin fluctuations
in the superconducting phase of
![]() may be
obtained by examination of the antiferromagnetic insulating compound
may be
obtained by examination of the antiferromagnetic insulating compound
![]() .
The structures of
.
The structures of
![]() and
and
![]() appear in Fig. 2.9 and the phase diagram for
YBa2Cu3Ox
(6 < x < 7) appears in Fig. 2.10.
In reference
to Fig. 2.9(a), the
Cu(1) or Cu-O chain layer of
appear in Fig. 2.9 and the phase diagram for
YBa2Cu3Ox
(6 < x < 7) appears in Fig. 2.10.
In reference
to Fig. 2.9(a), the
Cu(1) or Cu-O chain layer of
![]() consists entirely of Cu1+ ions. The singly ionized Cu ions have no
magnetic moment. Oxygen doping places O ions along the b-axis, resulting
in a progressive conversion of Cu1+ into Cu2+
with the development of holes in the 3d-shell of the Cu ions [59].
consists entirely of Cu1+ ions. The singly ionized Cu ions have no
magnetic moment. Oxygen doping places O ions along the b-axis, resulting
in a progressive conversion of Cu1+ into Cu2+
with the development of holes in the 3d-shell of the Cu ions [59].
 |
The Cu(2) or CuO2 planes of
![]() have predominantly Cu2+ ions. Each Cu gives up two electrons;
an electron from the 4s-shell and the other from the 3d-shell.
The absence of an electron in the 3d-shell (a hole) results in a
net magnetic moment (spin) on the Cu ions in this layer. Oxygen
cannot easily be removed or added to the CuO2 planes. The oxygen
concentration can be varied appreciably only in the Cu-O chains.
As mentioned, adding oxygen converts the copper ions in the Cu-O chains from
Cu1+ to Cu2+. Beyond
have predominantly Cu2+ ions. Each Cu gives up two electrons;
an electron from the 4s-shell and the other from the 3d-shell.
The absence of an electron in the 3d-shell (a hole) results in a
net magnetic moment (spin) on the Cu ions in this layer. Oxygen
cannot easily be removed or added to the CuO2 planes. The oxygen
concentration can be varied appreciably only in the Cu-O chains.
As mentioned, adding oxygen converts the copper ions in the Cu-O chains from
Cu1+ to Cu2+. Beyond
![]() it is believed that adding oxygen is equivalent to adding holes to
the CuO2 planes. The oxygen which is randomly
added to the chains becomes O2- by trapping two electrons which are
believed to originate from the creation of two holes in the oxygens of
an adjacent CuO2 plane. However, Hall coefficient measurements suggest
that holes may also be forming in the chains [23].
it is believed that adding oxygen is equivalent to adding holes to
the CuO2 planes. The oxygen which is randomly
added to the chains becomes O2- by trapping two electrons which are
believed to originate from the creation of two holes in the oxygens of
an adjacent CuO2 plane. However, Hall coefficient measurements suggest
that holes may also be forming in the chains [23].
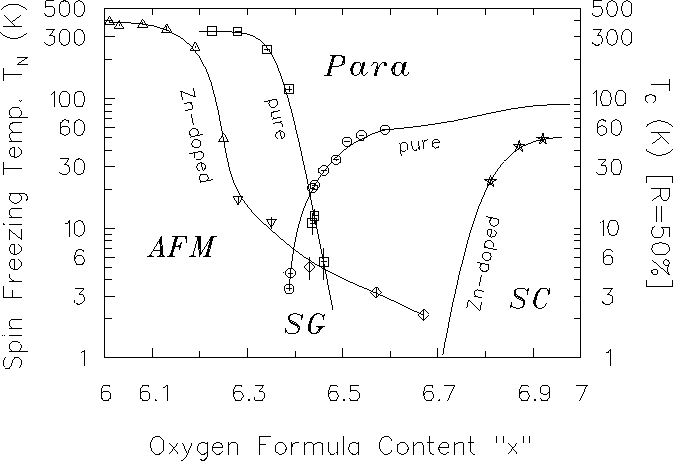
Neutron difffraction and muon precession experiments indicate that the
Cu moments are antiferromagnetically aligned in
![]() below the Neel temperature TN (see Fig. 2.10).
The Cu2+ spins (i.e. spin 1/2 holes)
in the CuO2 planes are coupled antiferromagnetically through a
superexchange process with the oxygen ions. The O2- ions themselves
have no net magnetic moment. At sufficiently low temperatures, the Cu ions
in the chains also become antiferromagnetically ordered and couple with
the Cu2+ ions in adjacent CuO2 planes [18]. In view
of this, the Cu1+ labelling of the chain layer Cu ions may not
be entirely accurate.
Neutron and Raman scattering
experiments suggest that the exchange interactions within the CuO2planes are much greater than the coupling between adjacent layers. This
is likely due to the greater separation between Cu ions in the
vertical direction and a lack of O2- ions between adjacent CuO2planes. The difference between strengths of the interplanar and
intraplanar couplings means that
below the Neel temperature TN (see Fig. 2.10).
The Cu2+ spins (i.e. spin 1/2 holes)
in the CuO2 planes are coupled antiferromagnetically through a
superexchange process with the oxygen ions. The O2- ions themselves
have no net magnetic moment. At sufficiently low temperatures, the Cu ions
in the chains also become antiferromagnetically ordered and couple with
the Cu2+ ions in adjacent CuO2 planes [18]. In view
of this, the Cu1+ labelling of the chain layer Cu ions may not
be entirely accurate.
Neutron and Raman scattering
experiments suggest that the exchange interactions within the CuO2planes are much greater than the coupling between adjacent layers. This
is likely due to the greater separation between Cu ions in the
vertical direction and a lack of O2- ions between adjacent CuO2planes. The difference between strengths of the interplanar and
intraplanar couplings means that
![]() exhibits a quasi
two-dimensional
magnetic behaviour. Furthermore, the measured maximum magnetic moment
on the Cu ions is substantially smaller than what one would expect for
a localized Cu2+ ion. This may be due to the
enhanced thermal fluctuations associated with a two-dimensionally
ordered system [18].
exhibits a quasi
two-dimensional
magnetic behaviour. Furthermore, the measured maximum magnetic moment
on the Cu ions is substantially smaller than what one would expect for
a localized Cu2+ ion. This may be due to the
enhanced thermal fluctuations associated with a two-dimensionally
ordered system [18].
It is a widely accepted belief that the electrons responsible for conduction in the copper-oxide superconductors are more or less confined to the CuO2 planes [52]. If this is the case then it is plausible that these electrons are paired by way of a two-dimensional system of antiferromagnetic spin fluctuations. The next obvious question to ask is,
``Do these spin fluctuations persist in the superconducting phase?''
Raman and neutron scattering measurements suggest that the magnetic fluctuations do indeed survive into the superconducting state. The spin-correlation length is substantially diminished in the superconducting state, but the amplitude of the magnetic moments is not greatly diminished [18]. Furthermore, NMR data taken above Tc indicate the presence of two-dimensional antiferromagnetic spin fluctuations arising from the nearly localized Cu2+ d-orbitals in the CuO2 planes.
It is difficult to give an intuitive description of pairing due to spin-fluctuation exchange. It is clear that a single hole will help destroy the antiferromagnetic order. However it is less clear whether it will attract or repel a second hole with the same or opposite spin. The answers to these questions seem to depend very much on the regions of k-space and r-space considered [60].
Weak-coupling calculations of the normal and superconducting state
properties have been
carried out [1,57,82]
for an antiferromagnetic spin-fluctuation induced interaction
between quasiparticles on a two-dimensional square lattice.
Such a two-dimensional model is at best an approximation to the behaviour
of the three-dimensional
![]() compound.
Nevertheless, these calculations yield
a value of the transition temperature Tc which is near 90K and
a superconducting pairing state with
dx2 - y2 symmetry.
For this pairing state the energy gap is of the form:
compound.
Nevertheless, these calculations yield
a value of the transition temperature Tc which is near 90K and
a superconducting pairing state with
dx2 - y2 symmetry.
For this pairing state the energy gap is of the form:
The superconducting gap originating from the spin-fluctuation mediated
interaction has a momentum (or k) dependence, in contrast to the
phonon-frequency dependence
of the gap associated with an electron-phonon
interaction.
It is clear from Eq. (2.31)
that the excitation gap vanishes when
![]() .
Fig. 2.11
shows the four nodes which result
along the diagonals in the Brillouin zone at the Fermi surface.
In three-dimensional k-space the gap vanishes along four nodal
lines running parallel to the kz-axis for a cylindrical Fermi
surface, or along four nodal lines joining the north and south
poles for a spherical Fermi surface (see Fig. 2.12).
Because of these nodal lines, there will be
considerably more quasiparticle excitations
at low temperatures compared to conventional s-wave superconductors.
Thus even at T=0K there is a quasiparticle
contribution to the supercurrent [61].
For
.
Fig. 2.11
shows the four nodes which result
along the diagonals in the Brillouin zone at the Fermi surface.
In three-dimensional k-space the gap vanishes along four nodal
lines running parallel to the kz-axis for a cylindrical Fermi
surface, or along four nodal lines joining the north and south
poles for a spherical Fermi surface (see Fig. 2.12).
Because of these nodal lines, there will be
considerably more quasiparticle excitations
at low temperatures compared to conventional s-wave superconductors.
Thus even at T=0K there is a quasiparticle
contribution to the supercurrent [61].
For
![]() which is highly anisotropic,
a cylindrical
Fermi surface with no gap in the kz direction
seems like a plausible description.
However, it has been
suggested that the cross-section of the Fermi surface in
which is highly anisotropic,
a cylindrical
Fermi surface with no gap in the kz direction
seems like a plausible description.
However, it has been
suggested that the cross-section of the Fermi surface in
![]() is not a perfect circle.
If this is the case, then the pairing state can have d-wave symmetry
but not give rise to nodes in the gap [49].
is not a perfect circle.
If this is the case, then the pairing state can have d-wave symmetry
but not give rise to nodes in the gap [49].
To gain a qualitative understanding of the symmetry in Fig. 2.11,
consider
the two-dimensional square lattice of antiferromagnetically ordered
spins depicted in Fig. 2.13.
In real space
nearest-neighbor spins are separated by the lattice constant a.
Such an arrangement is a simplified model of the CuO2 planes in
![]() .
In the
.
In the
![]() compound,
compound,
![]() ,
so that the CuO2 planes are almost square and the
localized spins of Fig. 2.13
correspond to the antiferromagnetically-correlated
spin fluctuations associated with the Cu2+ d-orbitals. In the
derivation of Eq. (2.31), a spin-spin correlation function
(electronic spin susceptibility) was chosen
which gave a good quantitative fit to
NMR measurements of the Knight shift and the spin-lattice relaxation
rates of 63Cu, 17O and 89Y nuclei in
,
so that the CuO2 planes are almost square and the
localized spins of Fig. 2.13
correspond to the antiferromagnetically-correlated
spin fluctuations associated with the Cu2+ d-orbitals. In the
derivation of Eq. (2.31), a spin-spin correlation function
(electronic spin susceptibility) was chosen
which gave a good quantitative fit to
NMR measurements of the Knight shift and the spin-lattice relaxation
rates of 63Cu, 17O and 89Y nuclei in
![]() [82]. The electronic spin susceptibility is representative
of the strength of the spin-fluctuation-mediated pairing potential.
This function is strongly peaked at the nesting wave
vector
[82]. The electronic spin susceptibility is representative
of the strength of the spin-fluctuation-mediated pairing potential.
This function is strongly peaked at the nesting wave
vector
![]() in the first
Brillouin zone. For an s-wave gap, the electronic spin susceptibility is
suppressed at
in the first
Brillouin zone. For an s-wave gap, the electronic spin susceptibility is
suppressed at
![]() [2].
[2].
To understand the significance of ![]() ,
consider first the phase-space
restrictions on the electron-electron scattering rate for a conventional
electron gas assuming a cylindrical Fermi surface.
At T=0K the Fermi cylinder is full
and there are no electrons to scatter from such that energy and momentum
are conserved.
For T > 0K, an excited electron with energy
different than EF can scatter into a shell of partially occupied
levels centered about EF in
,
consider first the phase-space
restrictions on the electron-electron scattering rate for a conventional
electron gas assuming a cylindrical Fermi surface.
At T=0K the Fermi cylinder is full
and there are no electrons to scatter from such that energy and momentum
are conserved.
For T > 0K, an excited electron with energy
different than EF can scatter into a shell of partially occupied
levels centered about EF in ![]() -space. That is to say,
the range of momenta available to the scattered electron is proportional
to the temperature T [47].
This situation is depicted in two dimensions in
Fig. 2.14(a), where the incoming
quasiparticle momenta are
-space. That is to say,
the range of momenta available to the scattered electron is proportional
to the temperature T [47].
This situation is depicted in two dimensions in
Fig. 2.14(a), where the incoming
quasiparticle momenta are ![]() and
and
![]() .
Any interaction between electrons changes
the momenta of the quasiparticles such that
.
Any interaction between electrons changes
the momenta of the quasiparticles such that
![]() .
Any orientation of the wave vector
.
Any orientation of the wave vector ![]() in
Fig. 2.14(a) will yield the same
available phase space for electron scattering
near the Fermi surface at a temperature T.
in
Fig. 2.14(a) will yield the same
available phase space for electron scattering
near the Fermi surface at a temperature T.
Consider now a nearly antiferromagnetic Fermi liquid with nesting vector
![]() as shown in Fig. 2.14(b).
In this nested-Fermi liquid, two electrons with
momenta (
as shown in Fig. 2.14(b).
In this nested-Fermi liquid, two electrons with
momenta (
![]() )
near the Fermi surface exchange the
antiferromagnetic spin fluctuation which has a sharp peak at
)
near the Fermi surface exchange the
antiferromagnetic spin fluctuation which has a sharp peak at ![]() .
The two electrons are subsequently scattered (by the oscillating potential
set up by the corresponding spin density wave) to states with wave
vectors (
.
The two electrons are subsequently scattered (by the oscillating potential
set up by the corresponding spin density wave) to states with wave
vectors (
![]() )
near opposite sides
of the Fermi surface. In this case
)
near opposite sides
of the Fermi surface. In this case
![]() .
As
illustrated in Fig. 2.14(b), the range of momenta
available to the scattering electron is greater than in the conventional
Fermi liquid of Fig. 2.14(a).
For all
.
As
illustrated in Fig. 2.14(b), the range of momenta
available to the scattering electron is greater than in the conventional
Fermi liquid of Fig. 2.14(a).
For all
![]() parallel
to the wave vectors
parallel
to the wave vectors
![]() and
and
![]() ,
the available phase space for scattering is the same. As
,
the available phase space for scattering is the same. As
![]() is rotated
away from these directions, the range
of momenta available to the scattering electron decreases so that it is
smallest when
is rotated
away from these directions, the range
of momenta available to the scattering electron decreases so that it is
smallest when
![]() .
The evolution of the wave vector
.
The evolution of the wave vector
![]() in Fig. 2.14(b)
maps out the gap function of Fig. 2.11.
This is demonstrated in Fig. 2.15.
As
in Fig. 2.14(b)
maps out the gap function of Fig. 2.11.
This is demonstrated in Fig. 2.15.
As
![]() is rotated away from
is rotated away from
![]() or
or
![]() ,
the
range of momenta available to scatter into
decreases and so does the magnitude of the energy gap.
,
the
range of momenta available to scatter into
decreases and so does the magnitude of the energy gap.
It should be noted that there are theories which predict
dx2-y2-wave pairing which are not based on spin
fluctuations [28]. Considering these, it seems appropriate to discuss
dx2-y2 symmetry as it pertains to the Fermi-surface geometry,
rather than to introduce the details of the theoretical calculations
which predict
dx2-y2-wave pairing from antiferromagnetic
spin fluctuations. The orientation of the Fermi surface in
Fig. 2.14(b) and Fig. 2.15 is that used
to explain commensurate peaks at
![]() in neutron experiments involving
in neutron experiments involving
![]() [62].
The corners of the Fermi surface are actually more rounded than they
appear in these figures.
The Fermi
surface for La2-xSrxCuO4 has more curvature in the sides and
is rotated
[62].
The corners of the Fermi surface are actually more rounded than they
appear in these figures.
The Fermi
surface for La2-xSrxCuO4 has more curvature in the sides and
is rotated
![]() from that
of
from that
of
![]() so that incommensurate
peaks are observed at
so that incommensurate
peaks are observed at
![]() in neutron experiments.
in neutron experiments.
Returning to
![]() and the notion of spin fluctuations,
if one assumes that a given oxygen nucleus is coupled predominantly
to the spins on its two nearest-neighbor Cu sites, then the Cu
spin-density of states is greatest near the Brillouin zone corners
and the notion of spin fluctuations,
if one assumes that a given oxygen nucleus is coupled predominantly
to the spins on its two nearest-neighbor Cu sites, then the Cu
spin-density of states is greatest near the Brillouin zone corners
![]() [56].
Also since the O nucleus is
resting between two oppositely directed Cu spins,
the transferred hyperfine field from the Cu moments cancels at the
O site so that the spin density vanishes there.
Thus the Cu spins relax the O nuclei so that the dominant contribution
to the spin susceptibility comes from the Cu2+ d-orbital
spin states.
Thus low temperature excitations may result
from the influence of the Cu spins on the superconducting carriers.
[56].
Also since the O nucleus is
resting between two oppositely directed Cu spins,
the transferred hyperfine field from the Cu moments cancels at the
O site so that the spin density vanishes there.
Thus the Cu spins relax the O nuclei so that the dominant contribution
to the spin susceptibility comes from the Cu2+ d-orbital
spin states.
Thus low temperature excitations may result
from the influence of the Cu spins on the superconducting carriers.
Opponents of the spin-fluctuation mechanism have argued that the
measured quasiparticle lifetimes in
![]() are much
too short for the quasiparticles to take advantage of this sort of
interaction [53].
Strong-coupling calculations (which normally imply a short quasiparticle
lifetime)
have been carried out. Results show that one still obtains
a Tc of 90K for
are much
too short for the quasiparticles to take advantage of this sort of
interaction [53].
Strong-coupling calculations (which normally imply a short quasiparticle
lifetime)
have been carried out. Results show that one still obtains
a Tc of 90K for
![]() ,
with a
dx2-y2pair gap [53]. Subsequent
calculations of the anomalous normal-state quasiparticle properties
in the corresponding strong-coupling regime have also been done
[53,63]. Results are consistent with experimental
measurements, indicating that the strong-coupling calculations are
reasonable.
,
with a
dx2-y2pair gap [53]. Subsequent
calculations of the anomalous normal-state quasiparticle properties
in the corresponding strong-coupling regime have also been done
[53,63]. Results are consistent with experimental
measurements, indicating that the strong-coupling calculations are
reasonable.
Theoretically a d-wave pairing state is appealing because it avoids
the strong on-site Coulomb repulsion which is inherent in an s-wave
pairing state. Also a spin-fluctuation pairing mechanism for the
high-Tc superconductors would not lead to a lattice instability
as may occur for an extremely strong electron-phonon interaction.
Unfortunately it is yet to be shown if the
dx2-y2 symmetry
evolves out of calculations for oxygen concentrations less than in
![]() .
Also a complete microscopic theory for
dx2-y2pairing is still unavailable. On the experimental front, attempts at determining
the pairing state in the copper-oxide superconductors have been
conflicting and inconclusive.
.
Also a complete microscopic theory for
dx2-y2pairing is still unavailable. On the experimental front, attempts at determining
the pairing state in the copper-oxide superconductors have been
conflicting and inconclusive.