

Next: 3 The SR Technique
Up: 2 The Characteristic Length
Previous: 2.4 The GL Penetration
In the Meissner state, 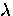 can be measured by excluded volume
techniques (such as microwave cavity perturbation), inductive methods
and far infrared reflectivity. The latter is a surface
measurement which can determine the absolute value of
can be measured by excluded volume
techniques (such as microwave cavity perturbation), inductive methods
and far infrared reflectivity. The latter is a surface
measurement which can determine the absolute value of  .In the vortex state,
.In the vortex state, 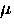 SR,
nuclear magnetic resonance (NMR) or small angle neutron scattering can
be used to measure the magnetic field inhomogeneity due to the vortex
lattice in the bulk of the sample,
from which an absolute value of
SR,
nuclear magnetic resonance (NMR) or small angle neutron scattering can
be used to measure the magnetic field inhomogeneity due to the vortex
lattice in the bulk of the sample,
from which an absolute value of 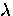 can be obtained.
can be obtained.
In contrast, there are few direct measurements of 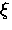 .Estimates of its magnitude can be obtained from the contribution
of fluctuations to measured quantities such as the
specific heat, susceptibility or conductivity.
Scanning tunneling microscopy (STM ) can be used
to measure the vortex-core radius r0 at the sample surface,
which provides an estimate
of
.Estimates of its magnitude can be obtained from the contribution
of fluctuations to measured quantities such as the
specific heat, susceptibility or conductivity.
Scanning tunneling microscopy (STM ) can be used
to measure the vortex-core radius r0 at the sample surface,
which provides an estimate
of 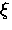
![[*]](foot_motif.gif) .
However, the coherence length is most often determined indirectly
from measurements
of the upper critical field, Hc2. At this field the vortices begin
to overlap and the superconductor undergoes a first order phase transition
into the normal state.
Since the radius of a normal vortex core is about the size of the coherence
length, then at Hc2 there is a
direct relationship with
.
However, the coherence length is most often determined indirectly
from measurements
of the upper critical field, Hc2. At this field the vortices begin
to overlap and the superconductor undergoes a first order phase transition
into the normal state.
Since the radius of a normal vortex core is about the size of the coherence
length, then at Hc2 there is a
direct relationship with 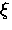 . In particular, from GL theory
. In particular, from GL theory
| 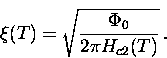 |
(69) |
In the high-Tc materials, Hc2 is extremely large (e.g. on the order
of 102 T in YBa2Cu3O7 at 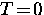 ) and is therefore
difficult to measure accurately. Measurements
are generally limited to temperatures near Tc where Hc2 is
considerably smaller (
) and is therefore
difficult to measure accurately. Measurements
are generally limited to temperatures near Tc where Hc2 is
considerably smaller (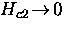 as
as 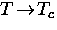 ).
However, near Tc thermal fluctuations of the vortex lines can depin or
melt the solid 3D vortex-lattice into a vortex liquid phase.
Rather than Hc2, what is often measured is the transition
of the ordered 3D vortex solid into a vortex fluid phase,
in which many of the vortices are free to move independently of each other.
The phenomenon is analogous to the way in which thermal
vibrations of water molecules cause ice to melt into water.
The problem of thermal fluctuations is most serious in short coherence
length superconductors with high transition temperatures. This is because
fluctuation effects become important when the thermal energy kB T
exceeds the condensation energy
).
However, near Tc thermal fluctuations of the vortex lines can depin or
melt the solid 3D vortex-lattice into a vortex liquid phase.
Rather than Hc2, what is often measured is the transition
of the ordered 3D vortex solid into a vortex fluid phase,
in which many of the vortices are free to move independently of each other.
The phenomenon is analogous to the way in which thermal
vibrations of water molecules cause ice to melt into water.
The problem of thermal fluctuations is most serious in short coherence
length superconductors with high transition temperatures. This is because
fluctuation effects become important when the thermal energy kB T
exceeds the condensation energy 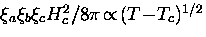 [43]. Here,
[43]. Here, 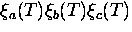 is the minimum volume
occupied by the fluctuation
and Hc is the thermodynamic
critical field. In the high-Tc materials,
thermal fluctuations are mainly responsible for the large variation in
reported values of
is the minimum volume
occupied by the fluctuation
and Hc is the thermodynamic
critical field. In the high-Tc materials,
thermal fluctuations are mainly responsible for the large variation in
reported values of 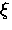 determined from Hc2 measurements.
A more appropriate way to determine
determined from Hc2 measurements.
A more appropriate way to determine 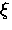 is to perform
measurements deep in the superconducting state, well away from
the strong fluctuation regime. This can be achieved with
is to perform
measurements deep in the superconducting state, well away from
the strong fluctuation regime. This can be achieved with 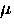 SR, a bulk
technique which is described next.
SR, a bulk
technique which is described next.



Next: 3 The SR Technique
Up: 2 The Characteristic Length
Previous: 2.4 The GL Penetration
![]() can be measured by excluded volume
techniques (such as microwave cavity perturbation), inductive methods
and far infrared reflectivity. The latter is a surface
measurement which can determine the absolute value of
can be measured by excluded volume
techniques (such as microwave cavity perturbation), inductive methods
and far infrared reflectivity. The latter is a surface
measurement which can determine the absolute value of ![]() .In the vortex state,
.In the vortex state, ![]() SR,
nuclear magnetic resonance (NMR) or small angle neutron scattering can
be used to measure the magnetic field inhomogeneity due to the vortex
lattice in the bulk of the sample,
from which an absolute value of
SR,
nuclear magnetic resonance (NMR) or small angle neutron scattering can
be used to measure the magnetic field inhomogeneity due to the vortex
lattice in the bulk of the sample,
from which an absolute value of ![]() can be obtained.
can be obtained.
![]() .Estimates of its magnitude can be obtained from the contribution
of fluctuations to measured quantities such as the
specific heat, susceptibility or conductivity.
Scanning tunneling microscopy (STM ) can be used
to measure the vortex-core radius r0 at the sample surface,
which provides an estimate
of
.Estimates of its magnitude can be obtained from the contribution
of fluctuations to measured quantities such as the
specific heat, susceptibility or conductivity.
Scanning tunneling microscopy (STM ) can be used
to measure the vortex-core radius r0 at the sample surface,
which provides an estimate
of ![]()
![[*]](foot_motif.gif) .
However, the coherence length is most often determined indirectly
from measurements
of the upper critical field, Hc2. At this field the vortices begin
to overlap and the superconductor undergoes a first order phase transition
into the normal state.
Since the radius of a normal vortex core is about the size of the coherence
length, then at Hc2 there is a
direct relationship with
.
However, the coherence length is most often determined indirectly
from measurements
of the upper critical field, Hc2. At this field the vortices begin
to overlap and the superconductor undergoes a first order phase transition
into the normal state.
Since the radius of a normal vortex core is about the size of the coherence
length, then at Hc2 there is a
direct relationship with ![]() . In particular, from GL theory
. In particular, from GL theory