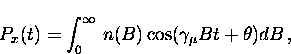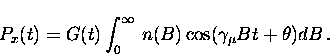


Next: 3.2.4 Four-Counter Geometry and
Up: 3.2 Measuring the Internal
Previous: 3.2.2 The Corrected Asymmetry
In the vortex state the muons experience a spatially varying magnetic field
due to the periodic arrangement of the vortices. In this case
the x-component of the time evolution of the total muon polarization is
| ![\begin{displaymath}
P_x(t) = \frac{1}{N} \sum_{i=1}^{N}
\cos [ \gamma_{\mu} B({\bf r}_i)t + \theta ] \, ,\end{displaymath}](img256.gif) |
(20) |
where the sum extends over all muon sites and 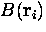 is the
local field at the site i. Ideally, the sum is replaced by an integral
so that
is the
local field at the site i. Ideally, the sum is replaced by an integral
so that
| 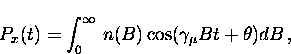 |
(21) |
where n(B) is the probability that the muon will precess at the
frequency 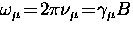 .
The muon spin polarization Px (t) decays with increasing time because of
the inhomogeneous field distribution.
Models of the field profile
.
The muon spin polarization Px (t) decays with increasing time because of
the inhomogeneous field distribution.
Models of the field profile
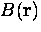 for a perfectly ordered vortex lattice will be discussed
in the next chapter.
for a perfectly ordered vortex lattice will be discussed
in the next chapter.
In a real superconductor there are other independent contributions to the
variation in the local field. These additional sources of field
inhomogeneity can be accounted for by multiplying the muon polarization
function by a ``relaxation function'' G(t) so that
| 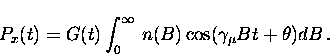 |
(22) |
The relaxation function G (t) describes the damping of the muon precession
signal which results from the additional sources of field inhomogeneity.
One such source is the nuclear dipolar fields in the sample.
A Gaussian relaxation function approximately describes the corresponding
damping of the muon precession signal [47]
| 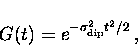 |
(23) |
where 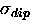 is the muon spin ``depolarization rate'' due to
the nuclear dipolar fields.
is the muon spin ``depolarization rate'' due to
the nuclear dipolar fields.
Signal damping also results from disorder in the vortex lattice.
According to Brandt [122] random disorder can be approximated
with a Gaussian relaxation function. The relaxation function which
contains the effects of the nuclear dipolar moments and the disorder
in the vortex lattice is
| 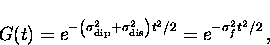 |
(24) |
where 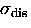 is the muon spin depolarization rate due to the
lattice disorder and
is the muon spin depolarization rate due to the
lattice disorder and 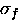 is the effective depolarization rate such that
is the effective depolarization rate such that
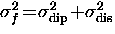 .
.



Next: 3.2.4 Four-Counter Geometry and
Up: 3.2 Measuring the Internal
Previous: 3.2.2 The Corrected Asymmetry
![\begin{displaymath}
P_x(t) = \frac{1}{N} \sum_{i=1}^{N}
\cos [ \gamma_{\mu} B({\bf r}_i)t + \theta ] \, ,\end{displaymath}](img256.gif)
![\begin{displaymath}
P_x(t) = \frac{1}{N} \sum_{i=1}^{N}
\cos [ \gamma_{\mu} B({\bf r}_i)t + \theta ] \, ,\end{displaymath}](img256.gif)