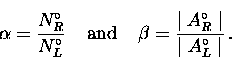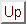


Next: 3.2.3 The Relaxation Function
Up: 3.2 Measuring the Internal
Previous: 3.2.1 The Raw Asymmetry
In practice, there are differences in the efficiency of the counters
and also geometrical misalignment of the counters. If the sensitivity
of the individual positron counters is not the same, the
normalization constant  , the maximum decay asymmetry
, the maximum decay asymmetry 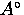 and the random background levels
and the random background levels 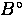 will not be the same in
all of the counters. The number of recorded
events in each counter also depends on the solid angle they subtend at
the sample. If the coverage of the solid angle is not maximized because
of counter misalignments, there will be a decrease in the number of
decay positrons detected. The raw asymmetry thus depends on the
variables
will not be the same in
all of the counters. The number of recorded
events in each counter also depends on the solid angle they subtend at
the sample. If the coverage of the solid angle is not maximized because
of counter misalignments, there will be a decrease in the number of
decay positrons detected. The raw asymmetry thus depends on the
variables
| 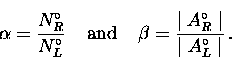 |
(18) |
In a superconductor, these variables are best determined
by fitting the muon spin precession signal in the normal state
where the magnetic field in the sample is more or less homogeneous.
The ``corrected asymmetry'' 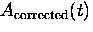 is obtained by substituting Eq. (3.18) into
Eq. (3.10) so that
is obtained by substituting Eq. (3.18) into
Eq. (3.10) so that
| 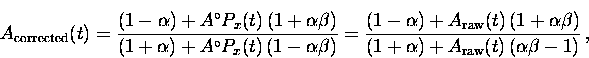 |
(19) |
where 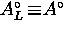 and
and 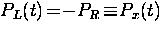 .
.



Next: 3.2.3 The Relaxation Function
Up: 3.2 Measuring the Internal
Previous: 3.2.1 The Raw Asymmetry
![]() , the maximum decay asymmetry
, the maximum decay asymmetry ![]() and the random background levels
and the random background levels ![]() will not be the same in
all of the counters. The number of recorded
events in each counter also depends on the solid angle they subtend at
the sample. If the coverage of the solid angle is not maximized because
of counter misalignments, there will be a decrease in the number of
decay positrons detected. The raw asymmetry thus depends on the
variables
will not be the same in
all of the counters. The number of recorded
events in each counter also depends on the solid angle they subtend at
the sample. If the coverage of the solid angle is not maximized because
of counter misalignments, there will be a decrease in the number of
decay positrons detected. The raw asymmetry thus depends on the
variables