BELIEVE ME NOT! -  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE


Next: Faraday's Law
Up: Maxwell's Equations
Previous: Maxwell's Equations
By now you are familiar with GAUSS' LAW in its integral form,
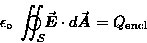 |
(22.1) |
where
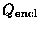 is the electric charge enclosed within
the closed surface
is the electric charge enclosed within
the closed surface 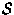 .
Except for the ``fudge factor''
.
Except for the ``fudge factor''
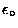 ,
which is just there to make the units
come out right, GAUSS' LAW is just a simple statement
that electric field ``lines'' are continuous except when they
start or stop on electric charges. In the absence of
``sources'' (positive charges) or ``sinks'' (negative charges),
electric field lines obey the simple rule, ``What goes in
must come out.'' This is what GAUSS' LAW says.
,
which is just there to make the units
come out right, GAUSS' LAW is just a simple statement
that electric field ``lines'' are continuous except when they
start or stop on electric charges. In the absence of
``sources'' (positive charges) or ``sinks'' (negative charges),
electric field lines obey the simple rule, ``What goes in
must come out.'' This is what GAUSS' LAW says.
There is also a GAUSS' LAW for the magnetic field
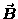 ;
we can write it the same way,
;
we can write it the same way,
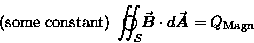 |
(22.2) |
where in this case
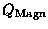 refers to the enclosed
magnetic charges, of which (so far) none have ever been found!
So GAUSS' LAW FOR MAGNETISM is usually written with a
zero on the right-hand side of the equation, even though
no one is very happy with this lack of symmetry between the
electric and magnetic versions.
refers to the enclosed
magnetic charges, of which (so far) none have ever been found!
So GAUSS' LAW FOR MAGNETISM is usually written with a
zero on the right-hand side of the equation, even though
no one is very happy with this lack of symmetry between the
electric and magnetic versions.
Figure:
An infinitesimal volume of space.
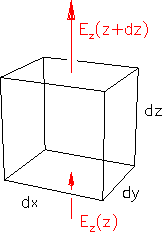 |
Suppose now we apply GAUSS' LAW to a small rectangular
region of space where the z axis is chosen to be in the
direction of the electric field, as shown in
Fig. 22.1.22.1
The flux of electric field into this volume
at the bottom is
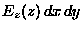 .
The flux out
at the top is
.
The flux out
at the top is
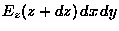 ;
so the net
flux out is just
;
so the net
flux out is just
![$[E_z(z+dz) - E_z(z)] \, dx \, dy$](img11.gif) .
The definition of the derivative of E with respect to z
gives us
.
The definition of the derivative of E with respect to z
gives us
![$[E_z(z+dz) - E_z(z)] = (\dbyd{E_z}{z}) \, dz$](img12.gif) where the partial derivative is used in acknowledgement of
the possibility that Ez may also vary with x and/or y.
GAUSS' LAW then reads
where the partial derivative is used in acknowledgement of
the possibility that Ez may also vary with x and/or y.
GAUSS' LAW then reads
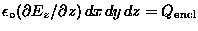 .
What is
.
What is
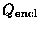 ? Well, in such a small region there is
some approximately constant charge density
? Well, in such a small region there is
some approximately constant charge density 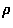 (charge per unit volume) and the volume of this region is
(charge per unit volume) and the volume of this region is
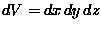 ,
so GAUSS' LAW reads
,
so GAUSS' LAW reads
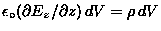 or just
or just
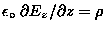 .
If we now allow for the possibility of electric flux entering
and exiting through the other faces (i.e.
.
If we now allow for the possibility of electric flux entering
and exiting through the other faces (i.e. 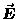 may also have x and/or y components), perfectly analogous
arguments hold for those components, with the resultant
``outflow-ness'' given by
may also have x and/or y components), perfectly analogous
arguments hold for those components, with the resultant
``outflow-ness'' given by
where the GRADIENT operator
 is shown in its
cartesian representation (in rectangular coordinates x,y,z).
It has completely equivalent representations in other coordinate systems
such as spherical (
is shown in its
cartesian representation (in rectangular coordinates x,y,z).
It has completely equivalent representations in other coordinate systems
such as spherical (
 )
or cylindrical coordinates,
but for illustration purposes the cartesian coordinates are simplest.
)
or cylindrical coordinates,
but for illustration purposes the cartesian coordinates are simplest.
We are now ready to write GAUSS' LAW in its compact
differential form,
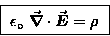 |
(22.3) |
and for the magnetic field, assuming no
magnetic charges ( MONOPOLES),
 |
(22.4) |
These are the first two of MAXWELL'S EQUATIONS.


Next: Faraday's Law
Up: Maxwell's Equations
Previous: Maxwell's Equations
Jess H. Brewer
1999-04-07
 - A SKEPTICs GUIDE
- A SKEPTICs GUIDE  - A SKEPTICs GUIDE
- A SKEPTICs GUIDE ![]() ;
we can write it the same way,
;
we can write it the same way,
![]() .
The flux out
at the top is
.
The flux out
at the top is
![]() ;
so the net
flux out is just
;
so the net
flux out is just
![]() .
The definition of the derivative of E with respect to z
gives us
.
The definition of the derivative of E with respect to z
gives us
![]() where the partial derivative is used in acknowledgement of
the possibility that Ez may also vary with x and/or y.
GAUSS' LAW then reads
where the partial derivative is used in acknowledgement of
the possibility that Ez may also vary with x and/or y.
GAUSS' LAW then reads
![]() .
What is
.
What is
![]() ? Well, in such a small region there is
some approximately constant charge density
? Well, in such a small region there is
some approximately constant charge density ![]() (charge per unit volume) and the volume of this region is
(charge per unit volume) and the volume of this region is
![]() ,
so GAUSS' LAW reads
,
so GAUSS' LAW reads
![]() or just
or just
![]() .
If we now allow for the possibility of electric flux entering
and exiting through the other faces (i.e.
.
If we now allow for the possibility of electric flux entering
and exiting through the other faces (i.e. ![]() may also have x and/or y components), perfectly analogous
arguments hold for those components, with the resultant
``outflow-ness'' given by
may also have x and/or y components), perfectly analogous
arguments hold for those components, with the resultant
``outflow-ness'' given by