In 1881, 78 years after Young introduced his two slit experiment, A.A. Michelson designed and built an interferometer using a similar principle. Originally Michelson designed his interferometer as a means to test for the existence of the ether, a hypothesized medium in which light propogated. Due in part to his efforts, the ether is no longer considered a viable hypothesis. But beyond this, Michelson's interferometer has become a widely used instrument for measuring the wavelength of light, for using the wavelength of a known light source to measure extremely small distances, and for investigating optical media.
Figure 8.1 shows a diagram of a Michelson interferometer.
The beam of light from the laser strikes the beam-splitter,
which reflects 50% of the incident light
and transmits the other 50%.
The incident beam is therefore split into two beams;
one beam is transmitted toward the movable mirror (M 
),
the other is reflected toward the fixed mirror (M 
).
Both mirrors reflect the light directly back
toward the beam splitter. Half the light from M
is reflected from the beam splitter to the viewing screen
and half the light from M is transmitted
through the beam splitter to the viewing screen.
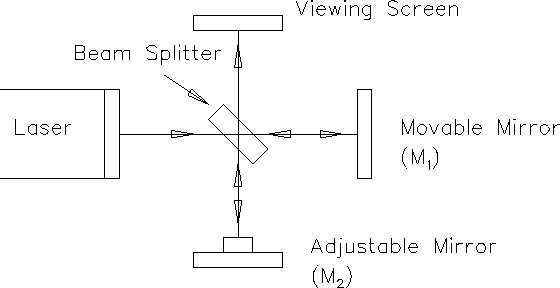
Figure 8.1: - Michelson interferometer.
In this way the original beam light is split and portions of the resulting beams are brought back together. Since the beams are from the same source, their phases are highly correlated. When a lens is placed between the laser source and the beams splitter, the light ray spreads out and an interference pattern of dark and bright rings, or fringes, is seen on the viewing screen.
Since the two interfering beams of light were split from the same initial beam, they were initially in phase. Their relative phase when they meet at any point on the viewing screen therefore depends on the difference in the length of their optical paths in reaching that point.
By moving M , the path length of one of the beams can be varied. Since the beam traverses the path between M and the beam splitter twice, moving M 1/4 wavelength
nearer the beam splitter will reduce the optical path of that beam by 1/2 wavelength.
The interference pattern will change; the radii of the maxima will be reduced so that they
occupy the position of the forma minima. If M is moved an additional 1/4 wavelength
closer to the beam splitter, the radii of the maxima will again be reduced so maxima and
minima trade positions, but this new arrangement will be indistinguishable from the original
pattern.
By slowly moving the mirror a measured distance 
, and counting m, the number of
times the fringe pattern is restored to its original state, the wavelength of the light 
can be calculated as:
If the wavelength of the light is known, the same procedure can be used to measure
.