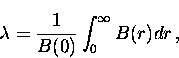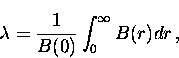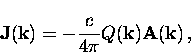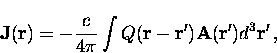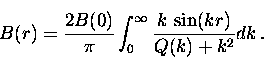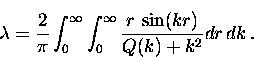


Next: 2.1.1 The London Penetration
Up: 2 The Characteristic Length
Previous: 2 The Characteristic Length
For a static magnetic field B(0) applied parallel to a planar
vacuum-to-superconducting interface, the magnetic penetration
depth can be defined as [1]
| 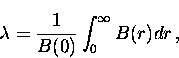 |
(1) |
where r is the distance into the superconductor measured from the
surface and
B(r) is a function describing the decay of the magnetic field
into the superconducting region.
The response of the superconductor to the magnetic field is usually
defined in terms of the expectation value of the induced supercurrent density,
which can be determined quantum mechanically [6].
The momentum-space
relation between the induced current and a static magnetic field
for an isotropic superconductor is
| 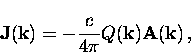 |
(2) |
where 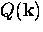 is a circularly symmetric
electromagnetic response kernel and
is a circularly symmetric
electromagnetic response kernel and
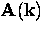 is the classical vector potential.
In general, the electromagnetic response kernel is a tensor.
In an AC field, J, Q and A are also functions of
the frequency
is the classical vector potential.
In general, the electromagnetic response kernel is a tensor.
In an AC field, J, Q and A are also functions of
the frequency 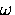 --however, in this thesis only
DC magnetic fields are used.
In real space the relation between the induced supercurrent density
and the vector potential can be written as
--however, in this thesis only
DC magnetic fields are used.
In real space the relation between the induced supercurrent density
and the vector potential can be written as
| 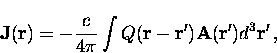 |
(3) |
where 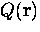 is the Fourier transform of
is the Fourier transform of 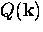 .In this case, J, Q and A are also functions of time
in an AC field.
The relation between Q (k) and an applied field B(0) is [1]
.In this case, J, Q and A are also functions of time
in an AC field.
The relation between Q (k) and an applied field B(0) is [1]
| 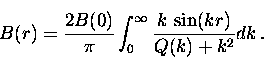 |
(4) |
Equation (2.1) and Eq. (2.4) can be combined
to give a general relation for 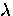 in terms of Q(k)
in terms of Q(k)
| 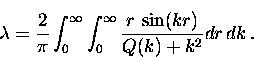 |
(5) |
Equation (2.5) is generally valid and can be used with the
kernel Q (k) corresponding to any theory.



Next: 2.1.1 The London Penetration
Up: 2 The Characteristic Length
Previous: 2 The Characteristic Length