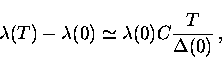


Next: 2.2 The Superconducting Coherence
Up: 2.1 The Magnetic Penetration
Previous: 2.1.2 The BCS Penetration
If there are line or point nodes in the energy
gap function 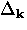 , a power law dependence is
expected, where
, a power law dependence is
expected, where
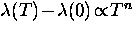 (
(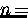 1, 2, 3 or 4)
[11,12].
The presence of the nodes on the Fermi surface allows quasiparticle
excitations to occur for an infinitesimal amount of thermal energy.
In particular, for the high-Tc superconductors there is strong evidence
that the energy gap has dx2-y2 symmetry. In this case the
energy gap function is given by
1, 2, 3 or 4)
[11,12].
The presence of the nodes on the Fermi surface allows quasiparticle
excitations to occur for an infinitesimal amount of thermal energy.
In particular, for the high-Tc superconductors there is strong evidence
that the energy gap has dx2-y2 symmetry. In this case the
energy gap function is given by
| 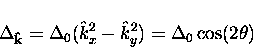 |
(27) |
where 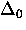 is the maximum value of the energy gap.
For this symmetry there are line nodes on the Fermi surface.
At low temperatures an approximate analytical expression can be obtained
for the magnetic penetration depth [13]
is the maximum value of the energy gap.
For this symmetry there are line nodes on the Fermi surface.
At low temperatures an approximate analytical expression can be obtained
for the magnetic penetration depth [13]
| 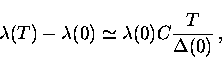 |
(28) |
where 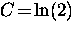 for a circular Fermi surface.
There are now many published measurements of the penetration depth
in high-Tc compounds, which support this linear-T behaviour.
Recent measurements in the Meissner state of high quality single crystals
of YBa2Cu3O
for a circular Fermi surface.
There are now many published measurements of the penetration depth
in high-Tc compounds, which support this linear-T behaviour.
Recent measurements in the Meissner state of high quality single crystals
of YBa2Cu3O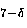 [14,15,16],
Bi2Sr2CaCu2O
[14,15,16],
Bi2Sr2CaCu2O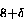 [17,18,19,20]
and magnetically aligned powders of crystalline
HgBa2Ca2Cu3O
[17,18,19,20]
and magnetically aligned powders of crystalline
HgBa2Ca2Cu3O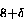 [21]
show a strong linear-T dependence for
[21]
show a strong linear-T dependence for 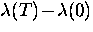 at low T.
Muon spin rotation (
at low T.
Muon spin rotation (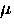 SR) measurements have determined that
SR) measurements have determined that 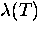 also changes linearly as a function of T in the vortex state of
YBa2Cu3O
also changes linearly as a function of T in the vortex state of
YBa2Cu3O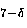 [2,3,5]
and La1.85Sr0.15CuO4 [22].
Experiments on the high-Tc materials which show T dependences
other than linear are often explained in terms of extrinsic effects.
For instance, in a
dx2-y2-wave superconductor, impurity scattering can change
the low-temperature behaviour of
[2,3,5]
and La1.85Sr0.15CuO4 [22].
Experiments on the high-Tc materials which show T dependences
other than linear are often explained in terms of extrinsic effects.
For instance, in a
dx2-y2-wave superconductor, impurity scattering can change
the low-temperature behaviour of 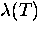 from a T to T2 dependence
[13,23].
This has been verified experimentally by substituting
small quantities of the non-magnetic impurity Zn2+ for Cu2+ in
YBa2Cu3O
from a T to T2 dependence
[13,23].
This has been verified experimentally by substituting
small quantities of the non-magnetic impurity Zn2+ for Cu2+ in
YBa2Cu3O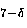 [24,25].
An exception in the high-Tc family appears to be the
electron-doped superconductors. For instance, measurements of
[24,25].
An exception in the high-Tc family appears to be the
electron-doped superconductors. For instance, measurements of
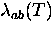 in Nd1.85Ce0.15CuO4
single crystals are consistent with s-wave BCS theory
and show no evidence of a linear-T term [26,27].
However, the large rare earth moments which are present
in the electron-doped high-Tc cuprates may have a large
effect on the measured
in Nd1.85Ce0.15CuO4
single crystals are consistent with s-wave BCS theory
and show no evidence of a linear-T term [26,27].
However, the large rare earth moments which are present
in the electron-doped high-Tc cuprates may have a large
effect on the measured 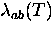 . This extrinsic effect
may mask the intrinsic nature of the superfluid which is common
to the hole-doped high-Tc materials.
. This extrinsic effect
may mask the intrinsic nature of the superfluid which is common
to the hole-doped high-Tc materials.



Next: 2.2 The Superconducting Coherence
Up: 2.1 The Magnetic Penetration
Previous: 2.1.2 The BCS Penetration
![]() , a power law dependence is
expected, where
, a power law dependence is
expected, where
![]() (
(![]() 1, 2, 3 or 4)
[11,12].
The presence of the nodes on the Fermi surface allows quasiparticle
excitations to occur for an infinitesimal amount of thermal energy.
In particular, for the high-Tc superconductors there is strong evidence
that the energy gap has dx2-y2 symmetry. In this case the
energy gap function is given by
1, 2, 3 or 4)
[11,12].
The presence of the nodes on the Fermi surface allows quasiparticle
excitations to occur for an infinitesimal amount of thermal energy.
In particular, for the high-Tc superconductors there is strong evidence
that the energy gap has dx2-y2 symmetry. In this case the
energy gap function is given by