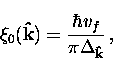


Next: 2.3 The Magnetic Field
Up: 2 The Characteristic Length
Previous: 2.1.3 Penetration Depth for dx-y-Wave
To explain numerous experimental results which
deviated from the predictions of the London theory, Pippard [28]
proposed the following general nonlocal relation for the supercurrent
response
| ![\begin{displaymath}
{\bf J_s}({\bf r}) = -\frac{3}{\xi_0}
\left( \frac{c}{4 \pi...
...f A} ({\bf r}^{\prime})]}{R^4}
\exp(-R/\xi) d^3 r^{\prime} \, ,\end{displaymath}](img100.gif) |
(29) |
where 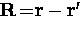 ,
,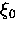 is the coherence length and
is the coherence length and 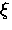 is an effective
coherence length related to the electron mean-free path l
through the equation
is an effective
coherence length related to the electron mean-free path l
through the equation
| 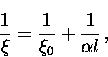 |
(30) |
where 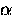 is a constant on the order of unity. For a pure
superconductor,
is a constant on the order of unity. For a pure
superconductor, 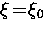 .The response of the superconductor to the applied magnetic field is
nonlocal, in the sense that the value of
.The response of the superconductor to the applied magnetic field is
nonlocal, in the sense that the value of 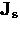 measured at a point
measured at a point 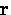 depends on the value of
depends on the value of 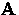 throughout a volume of radius
throughout a volume of radius 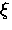 surrounding the point
surrounding the point 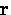 .The Pippard kernel relating the kth Fourier component of
.The Pippard kernel relating the kth Fourier component of 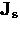 to
the vector potential
to
the vector potential 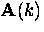 can be determined
from Eq. (2.30), and is given by
can be determined
from Eq. (2.30), and is given by
| ![\begin{displaymath}
Q_P (k) = \frac{\xi}{\xi_0 \lambda_L^2} \left\{ \frac{3}{2(k \xi)^3}
[(1+k^2 \xi^2) \tan^{-1} (k \xi) - k \xi] \right\} \, .\end{displaymath}](img107.gif) |
(31) |
QP (k) is always smaller than the London kernel QL (k). As a
result, substituting the expression for QP (k) into Eq. (2.5)
will always yield a value for 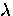 which is larger than
which is larger than 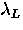 .In particular, for
.In particular, for 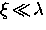
| 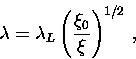 |
(32) |
and for 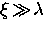
| 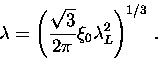 |
(33) |
Note that in the first limiting case, 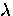 agrees with
the London prediction in a pure superconductor. On the other hand, the
second limiting case is completely independent of the electron mean-free
path. A superconductor described by the first equation, is called a
``type-II superconductor'', whereas one that is described
by the second equation is a ``type-I superconductor''.
agrees with
the London prediction in a pure superconductor. On the other hand, the
second limiting case is completely independent of the electron mean-free
path. A superconductor described by the first equation, is called a
``type-II superconductor'', whereas one that is described
by the second equation is a ``type-I superconductor''.
Using an argument based on the uncertainty principle, Pippard estimated that
the coherence length in a pure metallic superconductor is
| 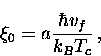 |
(34) |
where vf is the Fermi velocity and 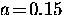 .In BCS theory, the response kernel
.In BCS theory, the response kernel 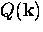 is similar to
that in Pippard theory. The BCS coherence length
is similar to
that in Pippard theory. The BCS coherence length
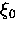 , is the range of the Fourier transform of
, is the range of the Fourier transform of 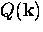 and is defined as
and is defined as
| 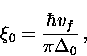 |
(35) |
where 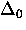 is the uniform energy gap at
is the uniform energy gap at 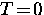 . Since
. Since
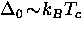 , the Pippard estimate is close to the
BCS coherence length.
In a conventional superconductor, vf and hence
, the Pippard estimate is close to the
BCS coherence length.
In a conventional superconductor, vf and hence 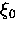 is large.
The bound electron pairs which make up the superfluid have a
spatial extent on the order of
is large.
The bound electron pairs which make up the superfluid have a
spatial extent on the order of 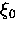 .
.
The high-Tc materials differ markedly from conventional superconductors
in that they have much smaller coherence lengths. Consequently, these
materials are in the extreme type-II limit.
The small value of the coherence length also
means that the high-Tc compounds are generally in the clean limit, where
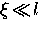 . Furthermore, both
fluctuation and boundary effects are much stronger in these short
. Furthermore, both
fluctuation and boundary effects are much stronger in these short
 superconductors.
In a dx2-y2-wave superconductor where the energy gap is
anisotropic, one must define an angle dependent coherence length
superconductors.
In a dx2-y2-wave superconductor where the energy gap is
anisotropic, one must define an angle dependent coherence length
| 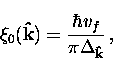 |
(36) |
where 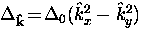 and
and 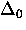 is the maximum value of the energy gap.
The divergence
of Eq. (2.37) along the node directions
is the maximum value of the energy gap.
The divergence
of Eq. (2.37) along the node directions
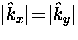 means that the extreme nonlocal
limit is obtained near the nodes (i.e.
means that the extreme nonlocal
limit is obtained near the nodes (i.e. 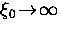 ).
Recently, Kosztin and Legget
[29] determined that nonlocal electrodynamics leads to
a crossover from a T to a T2 dependence for the penetration depth
in the Meissner state at extremely low temperatures. To observe this
experimentally, one must distinguish this effect from the T2
dependence expected from sample impurities. Both the
temperature and magnetic field dependence of
).
Recently, Kosztin and Legget
[29] determined that nonlocal electrodynamics leads to
a crossover from a T to a T2 dependence for the penetration depth
in the Meissner state at extremely low temperatures. To observe this
experimentally, one must distinguish this effect from the T2
dependence expected from sample impurities. Both the
temperature and magnetic field dependence of 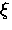 will be discussed later in
the thesis.
will be discussed later in
the thesis.



Next: 2.3 The Magnetic Field
Up: 2 The Characteristic Length
Previous: 2.1.3 Penetration Depth for dx-y-Wave
![\begin{displaymath}
{\bf J_s}({\bf r}) = -\frac{3}{\xi_0}
\left( \frac{c}{4 \pi...
...f A} ({\bf r}^{\prime})]}{R^4}
\exp(-R/\xi) d^3 r^{\prime} \, ,\end{displaymath}](img100.gif)
![\begin{displaymath}
{\bf J_s}({\bf r}) = -\frac{3}{\xi_0}
\left( \frac{c}{4 \pi...
...f A} ({\bf r}^{\prime})]}{R^4}
\exp(-R/\xi) d^3 r^{\prime} \, ,\end{displaymath}](img100.gif)
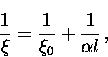
![\begin{displaymath}
Q_P (k) = \frac{\xi}{\xi_0 \lambda_L^2} \left\{ \frac{3}{2(k \xi)^3}
[(1+k^2 \xi^2) \tan^{-1} (k \xi) - k \xi] \right\} \, .\end{displaymath}](img107.gif)
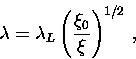
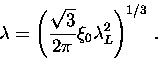
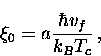
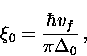
![]() . Furthermore, both
fluctuation and boundary effects are much stronger in these short
. Furthermore, both
fluctuation and boundary effects are much stronger in these short
![]() superconductors.
In a dx2-y2-wave superconductor where the energy gap is
anisotropic, one must define an angle dependent coherence length
superconductors.
In a dx2-y2-wave superconductor where the energy gap is
anisotropic, one must define an angle dependent coherence length